問16

(3)
[解説]
5進法の0.21を10進法で表すには、
$$ 0.21(5) = 5^{0}\times 0 + 5^{-1}\times 2 + 5^{-2}\times 1$$
$$ = 0 + \frac{2}{5^1} + \frac{1}{5^2}$$
$$ = \frac{11}{25} = 0.44(10)$$
といったようになります。
問17

(4)
[解説]
$$ \begin{eqnarray} \left\{\begin{array}{1} x^2 + 2kx + 1 = 0 …(1) \\ 2x^2 + x + 8k= 0 …(2)\end{array} \right.\end{eqnarray}$$
上記の連立方程式について考えます。
まず(1)について、解の公式より、
$$ x = -k \pm \sqrt{k^2-1} …(1)’$$
が得られます。ここで、共通の実数解を持つことから、根号の中身の$\sqrt{k^2-1}$は正となります。この条件に当てはまる選択肢は(3)と(4)の$k=-\frac{5}{4}$のみです。つまり、$k=-\frac{5}{4}$ということがわかります。
航大の総合Ⅱの数学では、このように正確に回答を求めなくても選択肢を絞っていくことができることがあります。積極的に選択肢を減らしていくことで、時間の節約にもつながていきましょう。
あとは$\alpha$が$2$か$-2$であるかの判断だけです。$k=-\frac{5}{4}$を(1)’に代入すると、
$$ x = \frac{5}{4} \pm \sqrt{\frac{9}{16}}$$
$$ = \frac{5}{4} \pm \frac{3}{4}$$
$$ = 2, \frac{1}{2}$$
と求められ、共通の実数解$\alpha$は2であることが分かります。
問18

(a) (1) (b) (1)
[解説]
(a)まず、正四面体とは下記のような図形です。立方体と混合してしまわないように注意しましょう。
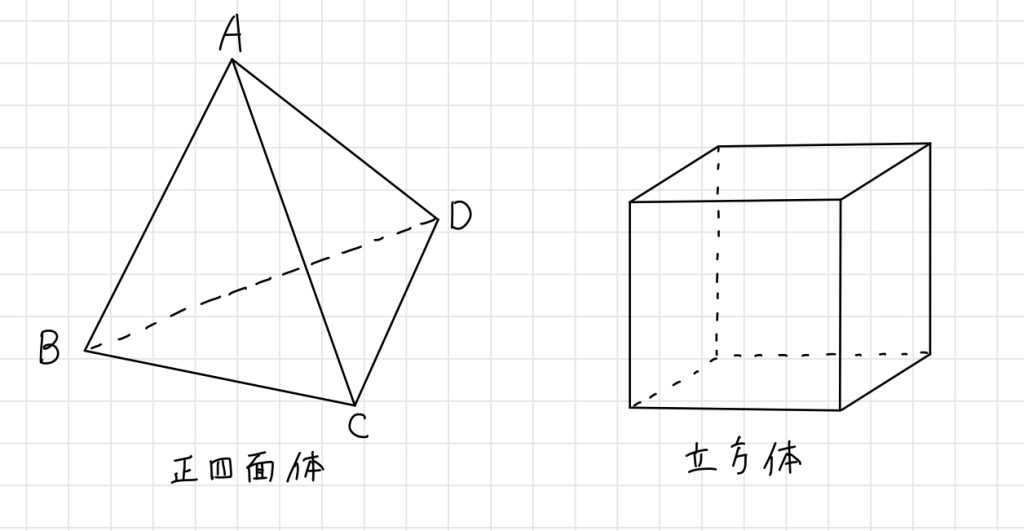
上記のような正四面体ABCDについて考えます。底面BCDは1辺の長さが3である正三角形であるため、
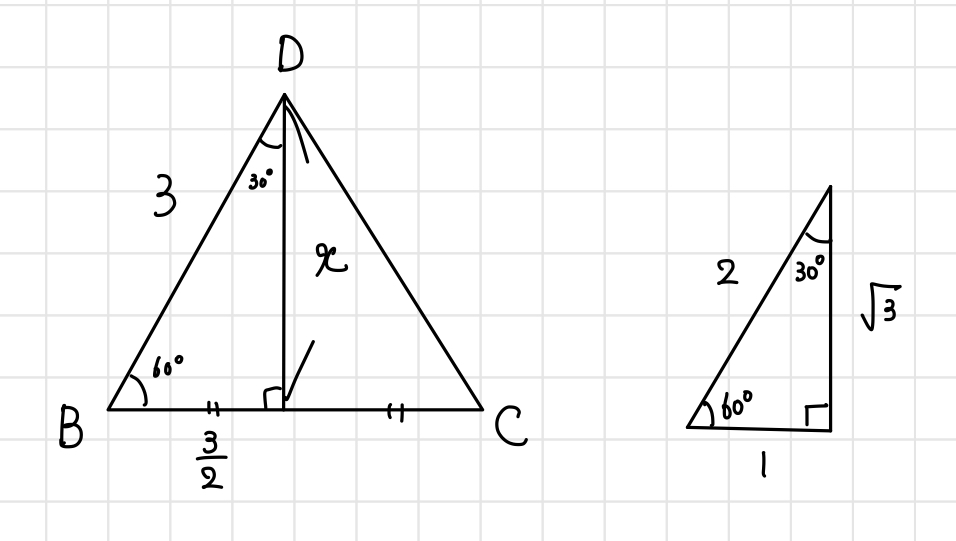
$x$の長さが分かれば底面積$S$が分かります。右図のような直角三角形の比を用いると、
$$1:\sqrt{3} = \frac{3}{2}:x$$
$$x = \frac{3\sqrt{3}}{2}$$
よって、底面積$S$は、
$$S = \frac{1}{2} \times 3 \times \frac{3\sqrt{3}}{2}$$
$$ = \frac{9\sqrt{3}}{4}$$
となります。
答え (1)
(b)正四面体ABCDの頂点Aから真下に底面BCDまで直線で直線を下ろし、底面BCDとの交点をA’とすると、A’は底面BCDの正三角形の重心位置となります。
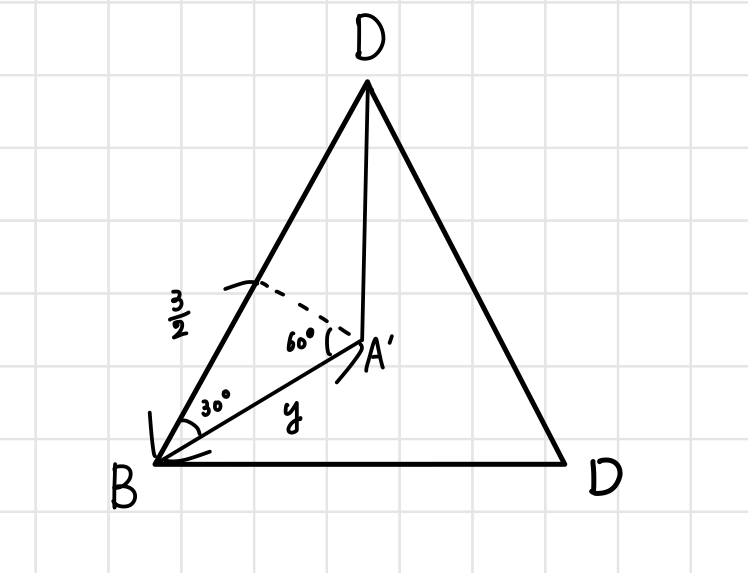
A’Bの長さを求めます。さっき用いた直角三角形の比の関係から、
$$\sqrt{3}:2 = \frac{3}{2}:A’B$$
$$A’B=\sqrt{3}$$
と分かります。これより、△ABA’のAA’の長さを求めます。
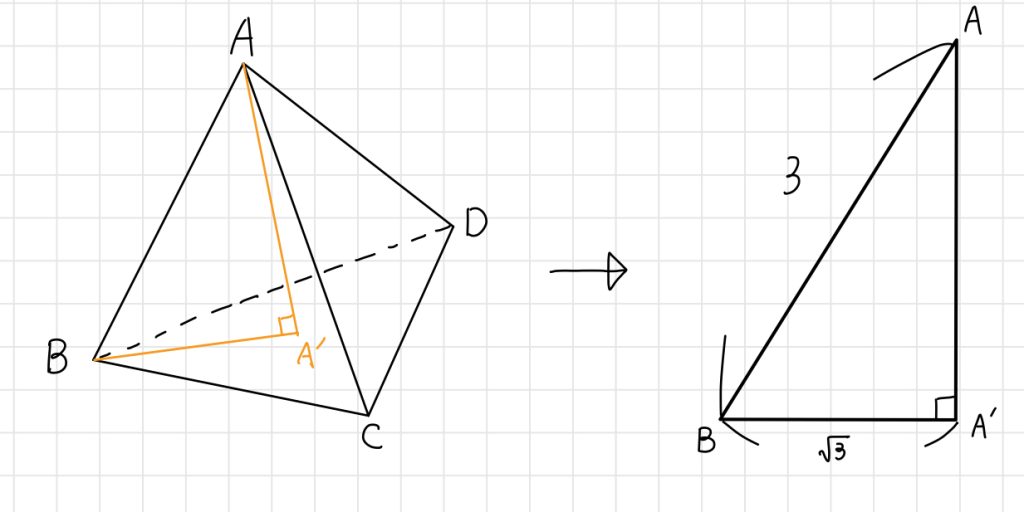
△ABA’は直角三角形であるため、
$$AA’ = \sqrt{3^2 – \sqrt{3}^2}$$
$$= \sqrt{9-3}$$
$$= \sqrt{6}$$
と分かります。よってこの正四面体の高さは$\sqrt{6}$です。
問19

(3)
[解説]
△ABCは二等辺三角形なので、
$$\angle ABC = \angle ACB$$
$$=\frac{(180^\circ – 36^\circ)}{2}$$
$$=72^\circ$$
です。ここで、$\angle ACD = \angle BCD$より、
$$\angle ACD = \frac{72^\circ}{2}$$
$$=36^\circ$$
です。三角形の外角の定理より、
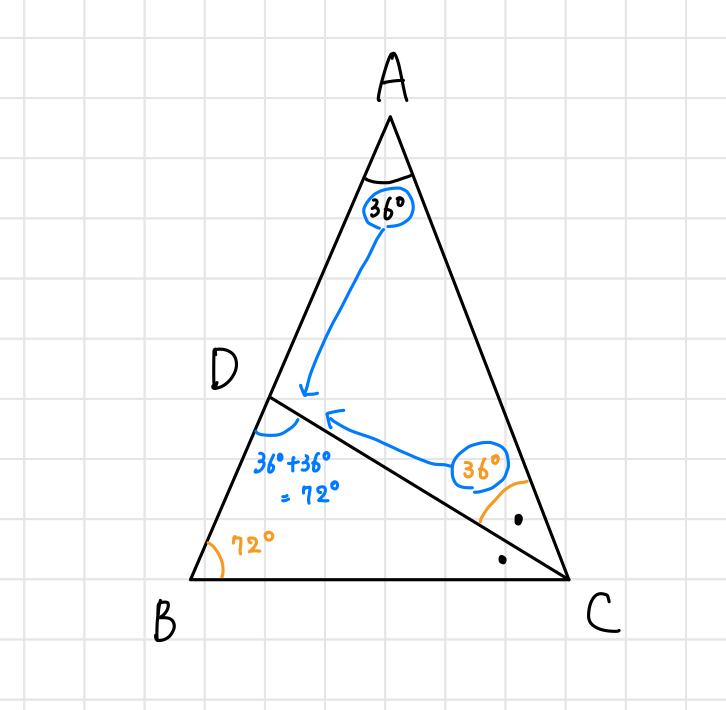
$$\angle CDB = 36^\circ + 36^\circ = 72^\circ$$
であることが分かります。すると、$\angle CBD = \angle CDB = 72^\circ$であり、△ABCと△CBDは3組(2組)の角が等しい相似な三角形であることが分かります。また、$\angle DAC = \angle DCA = 36^\circ$より、△DACは二等辺三角形であることから、$DA =DC$です。
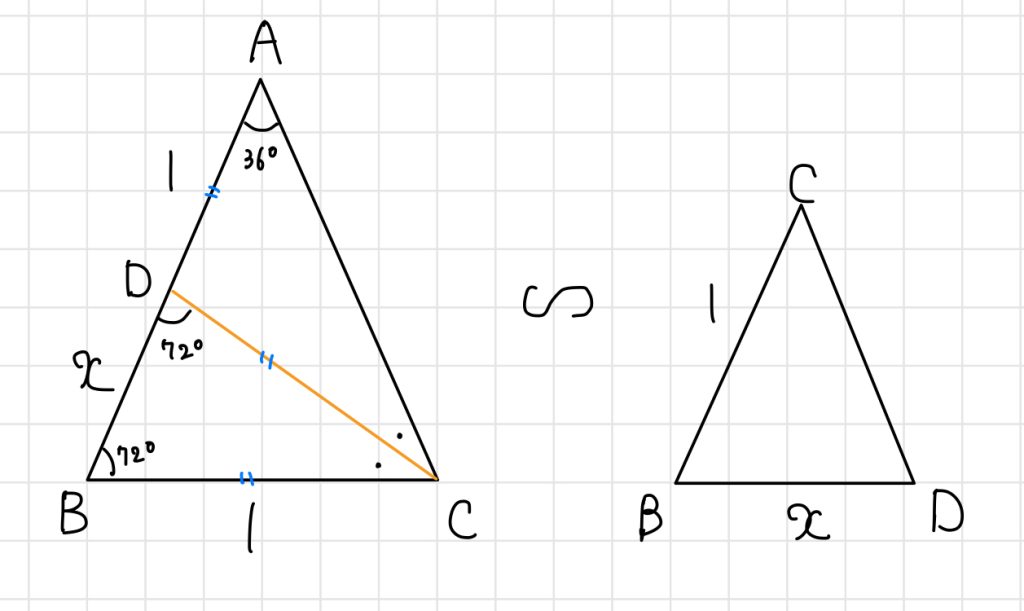
ここで、分かりやすいように、$BC=1$、$BD = x$とおくと、$AB = AD + DB = 1+x$となり、上図のような相似の関係から、
$$1+x : 1 = 1 : x$$
これを解くと、
$$x = \frac{-1 \pm \sqrt{5}}{2}$$
となり、$x>0$より、
$$x = \frac{-1 + \sqrt{5}}{2}$$
です。ここで$\theta = 36^\circ$とおくと、正弦定理より、
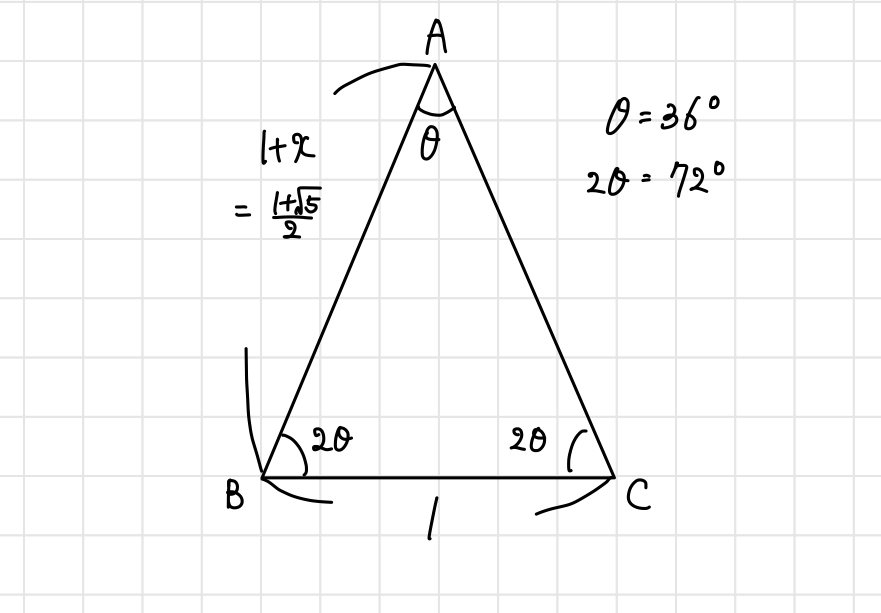
$$\frac{1}{\sin{\theta}} = \frac{\frac{1 + \sqrt{5}}{2}}{\sin{2\theta}}$$
$$\frac{1}{\sin{\theta}} = \frac{\frac{1 + \sqrt{5}}{2}}{2\sin{\theta} \cos{\theta}}$$
これを解くと、
$$\cos{\theta} = \frac{1+\sqrt{5}}{4}$$
となります。最後に三角関数の公式に当てはめると、
$$\sin{\theta} = \sqrt{1-\cos^2{\theta}}$$
$$=\sqrt{1-(\frac{1+\sqrt{5}}{4})^2}$$
$$=\frac{\sqrt{10-2\sqrt{5}}}{4}$$
となります。つまり、$\sin{\theta} = \sin{36^\circ} = \frac{\sqrt{10-2\sqrt{5}}}{4}$となります。
問20

(3)
[解説]
まず$a$について等式変形していくと以下のようになります。
$$a = \frac{\log_2 81 – \log_2 9}{\log_2 4}$$
$$ = \frac{\log_2 3^4 – \log_2 3^2}{\log_2 2^2}$$
$$ = \frac{4\log_2 3 – 2\log_2 3}{2\log_2 2}$$
$$ = \frac{2\log_2 3}{2}$$
$$=\log_2 3$$
$a=\log_2 3$とかなり見やすい形になりました。これについて、左辺を$a=\log2 2^a$と変形します。すると、
$$\log_2 2^a = log_2 3$$
よって、両辺を整理すると、
$$2^a = 3$$
となります。これを変形していきます。
$$2^a = 3$$
両辺4乗して、
$$2^{4a} = 3^4$$
$$\leftrightarrow \sqrt{2^{4a}} = \sqrt{3^4}$$
$$ = 3^2$$
$$=9$$
つまり、$\sqrt{2^{4a}} = 9$と分かります。
問21
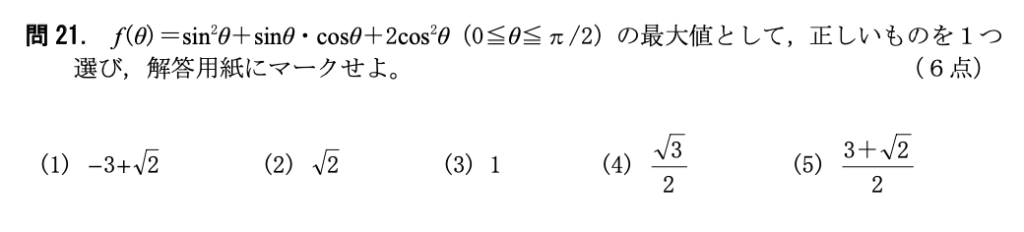
(5)
[解説]
$f(\theta)$を以下のように変形します。
$$f(\theta) = \sin^2{\theta} + \sin{\theta} \cos{\theta} + 2\cos^2{\theta}$$
$$ = \sin^2{\theta} + \cos^2{\theta} + \cos^2{\theta} + \sin{\theta} \cos{\theta}$$
$$ = 1 + \cos^2{\theta} + \sin{\theta} \cos{\theta}$$
$$ = 1 + \frac{1 + \cos{2\theta}}{2} + \frac{\sin{2\theta}}{2}$$
$$ = \frac{1}{2}(3 + \cos2{\theta} + \sin2{\theta})$$
ここで、$g\theta = \cos2{\theta} + \sin2{\theta} (0 \leq 2\theta \leq \pi)$とおき、$g(\theta)$を合成します。
$$g(\theta) = cos{2\theta} + sin{2\theta} \qquad (0 \leq 2\theta \leq \pi)$$
$$ = \sqrt{1^2 + 1^2}\sin{2\theta + \frac{\pi}{4} \qquad (\frac{\pi}{4} \leq 2\theta + \frac{\pi}{4} \leq \frac{5\pi}{4})}$$
$$ = \sqrt{2}\sin{2\theta + \frac{\pi}{4} \qquad (\frac{\pi}{4} \leq 2\theta + \frac{\pi}{4} \leq \frac{5\pi}{4})}$$
これより、$g(\theta)$の最大値は$\sqrt{2}$であることが分かります。よって、$f(\theta)$の最大値$f(\theta)_{max}$は、
$$f(\theta)_{max} = \frac{1}{2}(3 + \sqrt{2})$$
$$ = \frac{3+\sqrt{2}}{2}$$
となります。
問22

(1)
[解説]
$$ \begin{eqnarray} \left\{\begin{array}{1} x^{x+y} = y^2 …(1) \\ y^{x+y} = \sqrt{x} …(2)\end{array} \right.\end{eqnarray}$$
上記の連立方程式について、(1)、(2)式の両辺の対数を取ると、
$$ \begin{eqnarray} \left\{\begin{array}{1} (x+y)\log{x} = 2\log{y} …(1)’ \\ (x+y)\log{y} = \frac{1}{2}\log{x} …(2)’\end{array} \right.\end{eqnarray}$$
と書き換えることができます。(1)’式を$\log{y}$について整理すると、
$$\log{y} = \frac{1}{2}(x+y)\log{x} …(1)”$$
となり、(1)”式を(2)’式に代入すると、
$$(x+y)\frac{1}{2}(x+y)\log{x} = \frac{1}{2}\log{x}$$
となります。これを整理すると、
$$(x+y)^2 = 1$$
となり、これを満たすx、yの組み合わせは(1)のみです。
また解を求めることなく、答えに辿り着くことができました。このような問題は結構多いです。
問23

(5)
[解説]
与えられたグラフのx軸とy軸をひっくり返すと、下図のようになります。
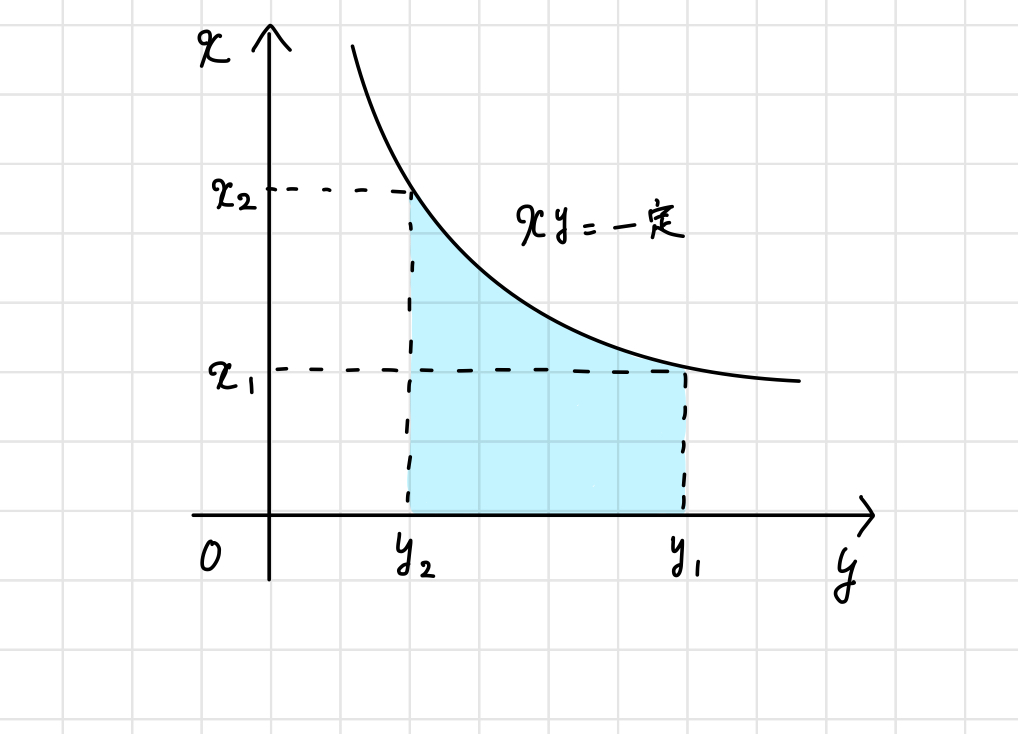
$xy=$一定という条件が与えられているため、$xy = k \; (k=const)$とおくと、
$$x = k\frac{1}{y}$$
と変形することができます。よって求める面積$S$は、
$$S = k \int_{y_2}^{y_1} \frac{1}{y} dy$$
$$ = k\left[ \log y \right]_{y_2}^{y_1}$$
$$ = k\log{\frac{y_1}{y_2}}$$
となります。
$k$はyの関数だから積分の外に出してしまうのは少し気持ちが悪い…と感じてしまうかもしれないですが、$xy$が定数という条件が与えられているため、このような変形をしても問題がありません。
ここで、$k = xy$より、
$$S = xy\log{\frac{y_1}{y_2}}$$
$$ = \log(\frac{y_1}{y_2})^{xy}$$
となります。
問24

(a) (5) (b) (2)
[解説]
(a)
内角の公式より、
$$\cos(\theta) = \frac{\overrightarrow{A} \cdot \overrightarrow{B}}{|\overrightarrow{A}| |\overrightarrow{B}|}$$
$$ = \frac{12 – 3}{\sqrt{5} \times 3\sqrt{5}} $$
$$ = \frac{3}{5}$$
となります。
(b)
$|\overrightarrow{A}+t\overrightarrow{B}|$について考えます。これを2乗すると、
$$|\overrightarrow{A}+t\overrightarrow{B}|^2$$
$$ = |\overrightarrow{A}|^2 + 2t\overrightarrow{A} \cdot \overrightarrow{B} + t^2 |\overrightarrow{B}|^2$$
$$ = 5 + 2t \times 9 + t^2 \times 45$$
$$ = 45t^2 + 9t + 5$$
$$ = 45(t^2 + \frac{2}{5}t) + 5$$
$$ = 45\{ (t+\frac{1}{5})^2 – \frac{1}{25} \} + 5$$
$$ = 45(t+\frac{1}{5})^2 + \frac{16}{5}$$
よって、$t=-\frac{1}{5}$のとき$|\overrightarrow{A}+t\overrightarrow{B}|^2$は最小、すなわち$|\overrightarrow{A}+t\overrightarrow{B}|$も最小となります。
問25

(3)
[解説]
まず与式の分母と分子の極限を取ってみます。すると、
分子:$\lim_{x \to 1} x-1 = 0$
分母:$\lim_{x \to 1} \sqrt{x+a}-b = \sqrt{1+a} \,- \, b$
となります。与式の極限値が0であれば問題ありませんが、今回は6が与えられているため、分子が0の場合、分母も0である不定形でないとおかしいことがわかります。そこで、$\sqrt{1+a} \,- \, b$が0となる組み合わせを選択肢から探すと、(3)のみであることがわかります。
一応答えを与式に入れてみて検算しておきましょう。a, bがわかればロピタルの定理が使えるため、
$$\lim_{x \to 1} \frac{x – 1}{\sqrt{x + 8} – 3}$$
$$ =\lim_{x \to 1} \frac{(x-1)’}{(\sqrt{x + 8} – 3)’}$$
$$ = 2\sqrt{1 + 8} = 6$$
となり、答えが正しいことがわかります。
この問題は数Ⅲに馴染みのない方にとっては意味のわからないない問題だったかもしれません。ただ、答えだけを求めるのであればそこまで難しい類の問題ではないので、解き方を覚えてしまうのもありかもしれません。


コメント