問16

(4)
[解説]
10進数を2進数で表現する際、最も直感的な方法は、$2^N$の足し算で表現する方法です。
$$93 = 1 \times 2^6 + 0 \times 2^5 + 1 \times 2^4 + 1 \times 2^3 + 1 \times 2^2 + 0 \times 2^1 + 1 \times 2^0$$
となります。2進数で表現する場合、係数を左から順に並べます。
$$93_{(10)} = 1011101_{(2)}$$
が答えとなります。
問17

(2)
[解説]
$$x^3 + y^3 = (x+y)^3 – 3xy(x+y)$$
$$x^2 + y^2 + z^2 = (x+y+z)^2 -2(xy + yz + zx)$$
$$x^3 + y^3 + z^3 = (x+y+z)(x^2 + y^2 + z^2 -xy – yz – zx)+3xyz$$

この変換公式はよく使うから覚えておいた方がええで。
上の公式を用いて、与式を分解して計算していきます。
\(x^2 + y^2 + z^2 = (x+y+z)^2 -2(xy + yz + zx)\)
\(=0^2 -2\times (-7) = 14\)
\(x^3 + y^3 + z^3 = (x+y+z)(x^2 + y^2 + z^2 -xy – yz – zx)+3xyz\)
\(=0\times (14-(-7)) + 3\times 6 = 18\)
\(x^4 + y^4 + z^4 = (x^2+y^2+z^2)^2 -2(x^2 y^2 + y^2 z^2 + z^2 x^2)\)
\(= (x^2+y^2+z^2)^2 – 2\{ (xy + yz + zx)^2 -2xyz(x + y+ z)\}\)
\(= 14^2 – 2\times \{(-7)^2 – 2\times 6 \times 0\} \)
\(= 196 – 2\times 49 = 98\)
よって、
\( (x^2 + y^2 + z^2) + (x^3 + y^3 + z^3) +(x^4 + y^4 + z^4) \)
\( = 14 + 18 + 98\)
\( = 130\)
となります。
問18

(5)
[解説]
(a)
$|\overrightarrow{a}+\overrightarrow{b}|=2$と$|\overrightarrow{a}-\overrightarrow{b}|$について、どちらも両辺を2乗します。
$$|\overrightarrow{a}+\overrightarrow{b}|^2 = |\overrightarrow{a}|^2 + 2\overrightarrow{a} \cdot \overrightarrow{b} + |\overrightarrow{b}|^2 = 4 \,\,\, …(1)$$
$$|\overrightarrow{a}\, \, – \,\, \overrightarrow{b}|^2 = |\overrightarrow{a}|^2 \, \, – \,\, 2\overrightarrow{a} \cdot \overrightarrow{b} + |\overrightarrow{b}|^2 = 4 \,\,\, …(2)$$
(1)式-(2)式より、
$$4\overrightarrow{a} \cdot \overrightarrow{b} = 0$$
よって、
$$\overrightarrow{a} \cdot \overrightarrow{b} = 0$$
となります。
(b)
$$|3\overrightarrow{a}\, \, – \,\, 2\overrightarrow{b}|^2 + |2\overrightarrow{a}\, \, – \,\, 3\overrightarrow{b}|^2$$
$$ = 9|\overrightarrow{a}|^2 \,\,-\,\, 12\overrightarrow{a} \cdot \overrightarrow{b} + 4|\overrightarrow{b} + 4|\overrightarrow{a}|^2 \,\,-\,\, 12\overrightarrow{a} \cdot \overrightarrow{b} + 9|\overrightarrow{b}|^2$$
$$= 13|\overrightarrow{a}|^2 \,\,-\,\, 24\overrightarrow{a} \cdot \overrightarrow{b} + 13|\overrightarrow{b}$$
(a)より、$\overrightarrow{a} \cdot \overrightarrow{b} = 0$であるため、$13(|\overrightarrow{a}|^2+|\overrightarrow{b}|^2)$について考えます。(1)式より、
$$|\overrightarrow{a}|^2 + 2\overrightarrow{a} \cdot \overrightarrow{b} + |\overrightarrow{b}|^2 = |\overrightarrow{a}|^2 + |\overrightarrow{b}|^2 = 4$$
です。よって、
$$13(|\overrightarrow{a}|^2+|\overrightarrow{b}|^2) = 13 \times 4=52$$
となります。
問19

(1)
[解説]
$6^x = 7^y = 42^z = A \,\, (A>0かつA\neq 1)$とおきます。これらを変形すると、
$$6^x = A \leftrightarrow x = \log_6{A} = \frac{1}{\log_A{6}}$$
$$7^y = A \leftrightarrow y = \log_7{A} = \frac{1}{\log_A{7}}$$
$$42^z = A \leftrightarrow z = \log_42{A} = \frac{1}{\log_A{42}}$$
が得られます。与式に代入すると、
$$\frac{1}{x} + \frac{1}{y} \,\,-\,\, \frac{1}{z} = \log_A{6} + \log_A{7} \,\,-\,\, \log_A{42}$$
$$ = \log_A{42} – \log_A{42}$$
$$= \log_A{1} = 0$$
となります。
問20

(2)
[解説]
まず$\theta = \frac{\pi}{5}$とおきます。これを以下のように変形していきます。
$$5\theta = \pi$$
$$3\theta = \pi – 2\theta$$
$$\sin{3\theta} = \sin{\pi-2\theta}$$
$$ = \sin{2\theta}$$
これを3倍角、2倍角の公式を用いて変形すると、
$$3\sin{\theta} – 4\sin^3{\theta} = 2\sin{\theta}\cos{\theta}$$
となります。$\theta = \frac{\pi}{5}$より、$\sin{\theta} \neq 0$であるため、両辺を$\sin{\theta}$で割ると、
$$3-4\sin^2{\theta} = 2\cos{\theta}$$
が得られます。これを$\cos{\theta}$のみの関数に変形すると、
$$3-4(1-\cos^2{\theta}) = 2\cos{\theta}$$
$$\leftrightarrow 4\cos^2{\theta} -2\cos{\theta} -1 = 0$$
となります。$\cos{\theta} > 0$より、
$$\cos{\theta} = \frac{1 + \sqrt{5}}{4}$$
となります。ここで半角の公式より、
$$\sin^2{\frac{\theta}{2}} = \frac{1-\cos{\theta}}{2}$$
$$ = \frac{3-\sqrt{5}}{8}$$
よって、
$$\sin{\frac{\theta}{2}} = \frac{1}{2} \sqrt{\frac{3-\sqrt{5}}{2}}$$
$$ = \frac{1}{4} \sqrt{6-2\sqrt{5}}$$
$$ = \frac{1}{4} \sqrt{(-1 + \sqrt{5})^2}$$
$$ = \frac{-1 + \sqrt{5}}{4}$$
となります。
問21
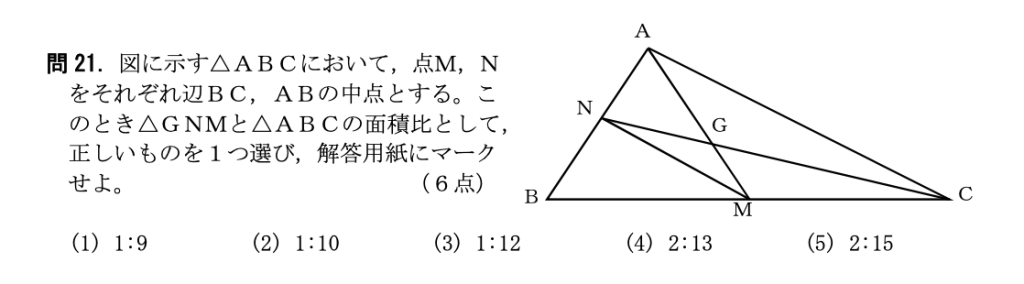
(3)
[解説]
BN = NA、BM = MCから中点連結定理より、MN//ACとMN=$\frac{1}{2}$ACが得られます。これより、△GMNと△GACは辺の比が1:2、すなわち面積の比が1:4であることが分かります。
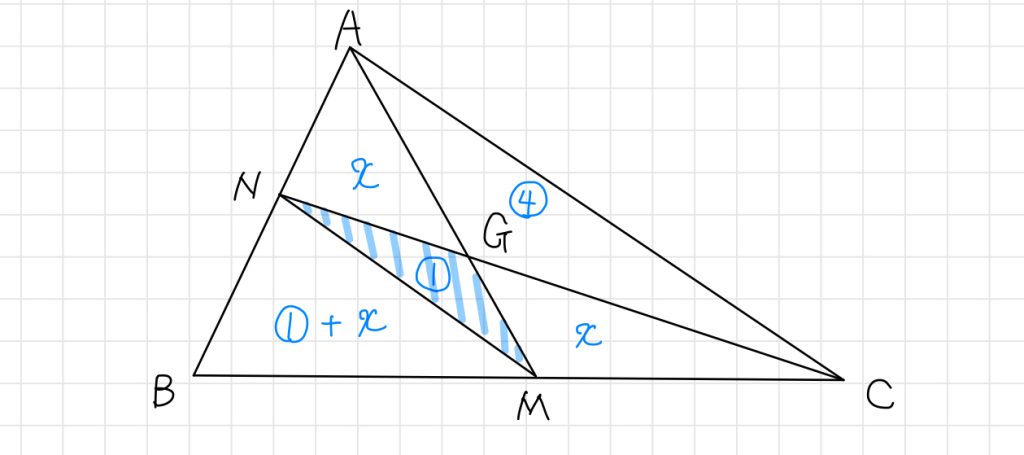
△GMNの面積を①とします。
次に△MABと△NBCについて考えます。BN = ANより、
△MBN = △MAN
またMB = MCより、
△MBN = △MCA
と分かります。つまり、△MAN = △MCAです。△GMNは共通であるため、△GAN = △GMC = xとおきます。
△BMNと△BCAについて、MN = $\frac{1}{2}$ACより、面積の比は1:3と分かります。△MBN = △MANより、
△MBN = △GMN + △GAN = ①+x
です。以上より、
①+x : ①+④+x+x = 1 : 3
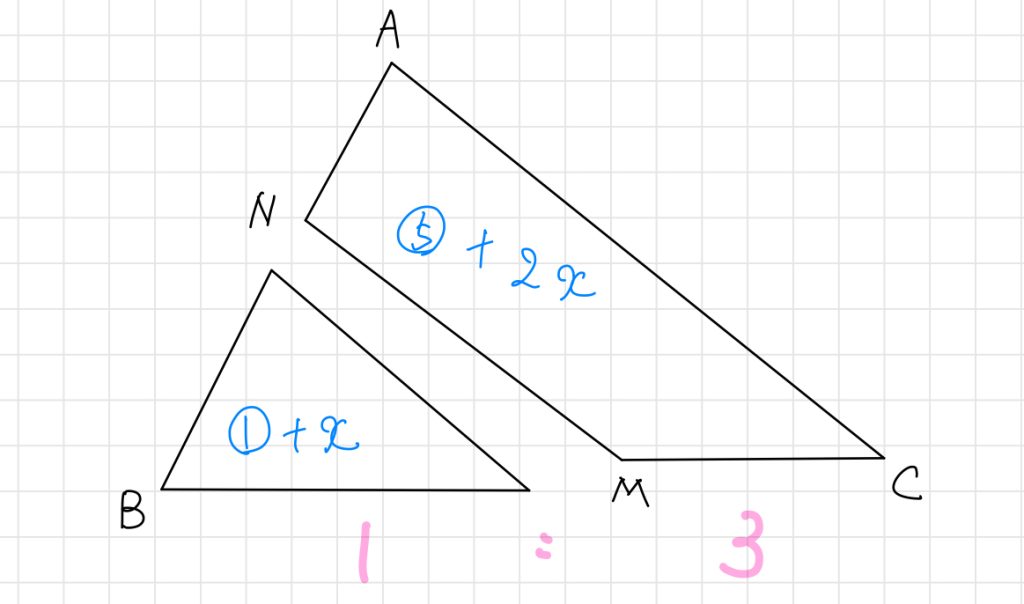
これを解くと、x = ②が得られます。これより、△ABCの面積は③+①+②+②+④ = 12 と分かりました。
よって、△GNM : △ABC = 1:12 です。
問22

(3)
[解説]
2つの解が$\sin{\theta}$と$\cos{\theta}$であるため、解と係数の関係より、
$$\sin{\theta} + \cos{\theta} = \frac{k}{2} \,\,\, …(1)$$
$$\sin{\theta}\cos{\theta} = \frac{\sqrt{3}}{4} \,\,\, …(2)$$
が得られます。$k$を求めるために(1)式を2乗します。
$$(\sin{\theta} + \cos{\theta})^2 $$
$$= \sin^2{\theta} + 2\sin{\theta}\cos{\theta} + \cos^2{\theta} = \frac{k^2}{4}$$
$$\leftrightarrow 1+2\times \frac{\sqrt{3}}{4} = \frac{k^2}{4}$$
$$\leftrightarrow k^2 = 4 + 2\sqrt{3}$$
$$ = (\sqrt{3} + 1)^2$$
$k>0$より、$k = (1+\sqrt{3})$となります。これを与式に代入すると、
$$4x^2 – 2(1 + \sqrt{3})x + \sqrt{3} = 0$$
$$(2x-\sqrt{3})(2x-1) = 0$$
$0 < \theta < \pi$より、$(\sin{\theta},\cos{\theta}) = (\frac{\sqrt{3}}{2}, \frac{1}{2}) \,\,\,or \,\,\,(\frac{1}{2}, \frac{\sqrt{3}}{2})$であることが分かります。
$\tan{\theta} = \frac{\sin{\theta}}{\cos{\theta}}$より、
$$\tan{\theta} = \sqrt{3} \,\,\,or \,\,\, \frac{1}{\sqrt{3}}$$
よって選択肢の中でこれに該当すのは、$\tan{\theta} = \sqrt{3}$です。
問23

(1)
[解説]
まず計算しやすいように低を揃えます。
$$\log_{\sqrt{y}}3 = \frac{\log_y{3}}{\log_y{\sqrt{y}}}$$
$$ = \frac{\log_y {3}}{\frac{1}{2}}$$
$$ = 2\log_y {3}$$
これを与式に戻して変形していきます。
$$2 + 2\log_y {3} < 4\log_y {3} + 2\log_y {(1-\frac{x}{2})}$$
$$\leftrightarrow 2 < 2\log_y {3} + 2\log_y {(1-\frac{x}{2})}$$
$$\leftrightarrow 1 < \log_y {3} + \log_y {(1-\frac{x}{2})}$$
$$\leftrightarrow \log_y {y} < \log_y {3(1-\frac{x}{2})}$$
つまり、
$$y < 3(1-\frac{x}{2})$$
$$\leftrightarrow \frac{3}{2}x + y <3$$
を満たす(x,y)の組み合わせは、(1)の(x,y) = (0, 2)のみです。
問24

(a) (3) (b) (5)
[解説]
半径r、高さhの直円柱について考えます。
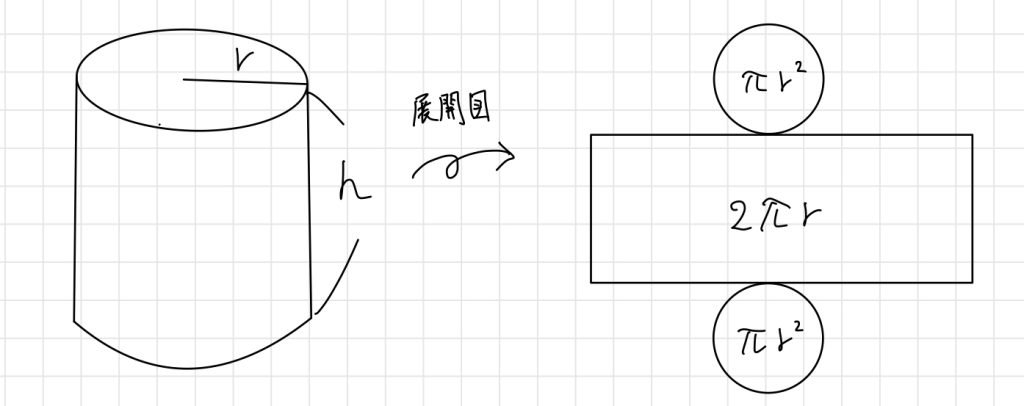
表面積:$S(r) = \pi r^2 + 2\pi rh + \pi r^2$
体積:$V(r) = \pi r^2 \times h$
ここで、表面積は$72\pi$であるため、
$$S(r) = 2\pi r^2 + 2\pi rh = 72\pi$$
すなわち、$$r^2 + rh = 36$$
です。$rh = 36 – r^2$を$V(r)$に代入すると、
$$V(r) = \pi r(36-r^2)$$
となります。$V(r)$の最大値を求めるために、$V(r)$のグラフを求めることにします。
$$V(r) = -\pi r^3 + 36\pi r$$
$$V'(r) = -3\pi r^2 + 36\pi = -3\pi(r^2-12)$$
増減表及びグラフは以下のようになります。
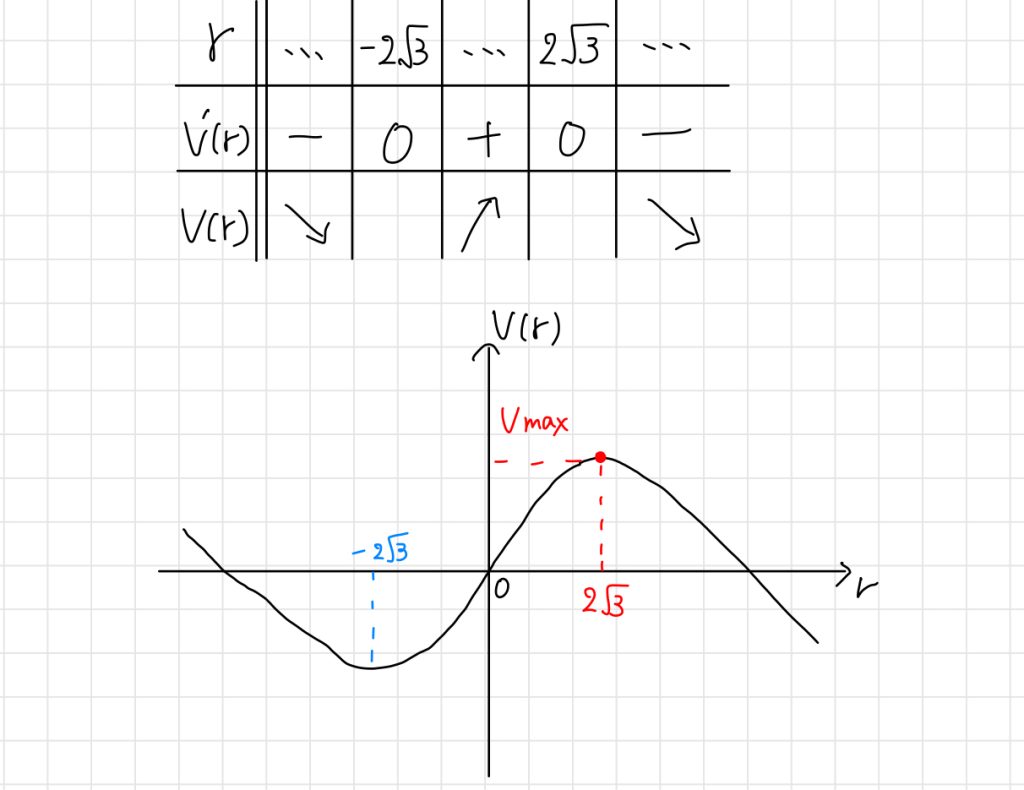
$r>0$より、体積$V(r)$を最大にする$r$は$2\sqrt{3}$です。
(b)
$$V(2\sqrt{3}) = \pi \times 2\sqrt{3} \times (36-12)$$
$$ =48\sqrt{3}\pi $$
となります。
問25

(2)
[解説]
$$\int_{1}^{2}\{(x-1)(x-2)\}^2 dx$$
$$ = \int_{1}^{2}\{(x-1)(x-1-1)\}^2 dx$$
ここで、$x-1 = A$とおきます。
$$\{(x-1)(x-1-1)\}^2$$
$$ = \{A(A-1)\}^2$$
$$ = (A^2-A)^2$$
$$ = A^4 – 2A^3 + A^2$$
となります。$A=x-1$を元に戻して計算を進めていきます。
$$\int_{1}^{2}\{(x-1)^4 – 2(x-1)^3 + (x-1)^2\}$$
$$= [\frac{1}{5}(x-1)^5 – \frac{2}{4}(x-1)^4 + \frac{1}{3}(x-1)^3]$$
$$ = \frac{1}{5} – \frac{1}{2} + \frac{1}{3}$$
$$ = \frac{1}{30}$$
となります。


コメント