問7

(a) (1) (b) (1)
[解説]
(a)(ア)気体中を伝わる音速は、「媒質の種類」や「温度」によって異なります。この穴埋めがわからなかったとしても、問題文を読むと、液体中と固体中では音速が異なることが読み取れるため、冷静に対処しましょう!
(イ)音速は空気中よりも液体や固体中の方が大きくなります。
気体中では音速は約$340 \,[m/s]$であるのに対し、水中では約$1500 \,[m/s]$、固体(鉄)中では$6000 \,[m/s]$にもなるそうです。
(ウ)音速を求める式は覚えておきましょう!
乾燥した空気の温度を$t[^\circ C]$とすると、音速$V \, [m/s]$は、
$$V = 331.5 + 0.6 \times t \, [m/s]$$
と表すことができます。もし覚えていなかった場合、地上で音速が$340\,[m/s]$程度であると覚えておけば、気温$25^\circ C$を代入し、計算してみると、(ウ)は0.6が最も適していると判断することもできます。知識が抜けていた場合は慌てることなく、自分が有している知識と照らし合わせながら答えを導き出す練習をしておくのもよいかもしれないですね!
(b)$15[^\circ C]$の乾燥した空気中を伝わる音速$V\,[m/s]$は、
$$V = 331.5 + 0.6 \times 15$$
$$ = 340.5 \,[m/s]$$
となります。波の伝わる速さを$v\,[m/s]$、波長を$\lambda\,[m]$、振動数を$f\,[Hz]$とすると、
$$v = f\times \lambda$$
と表すことができるため、求めたい波長は、
$$\lambda = \frac{v}{f}$$
$$ = \frac{340.5}{20 \times 10^3}$$
$$ = 17 \times 10^{-3}\,[m]$$
$$ = 1.7\,[cm]$$となります。
問8
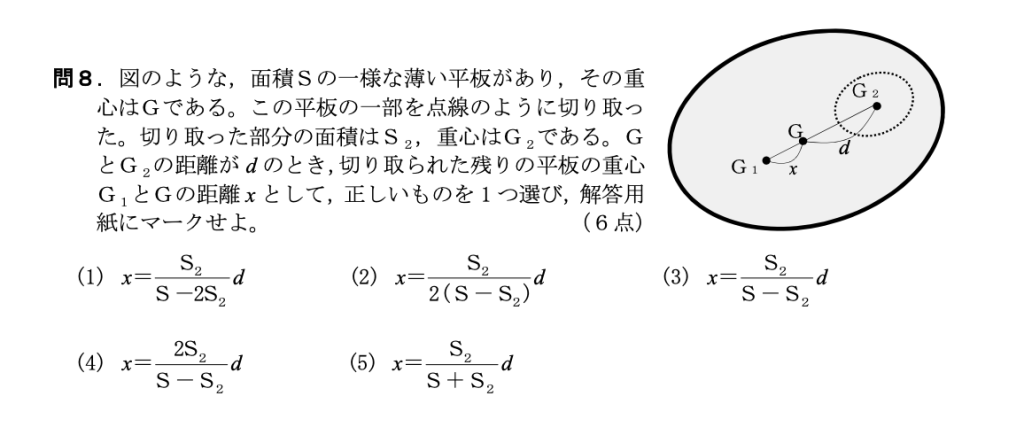
(3)
[解説]
面積S、質量Mの一様な平板を下図のように切り分けて、平板1と平板2と名付けます。
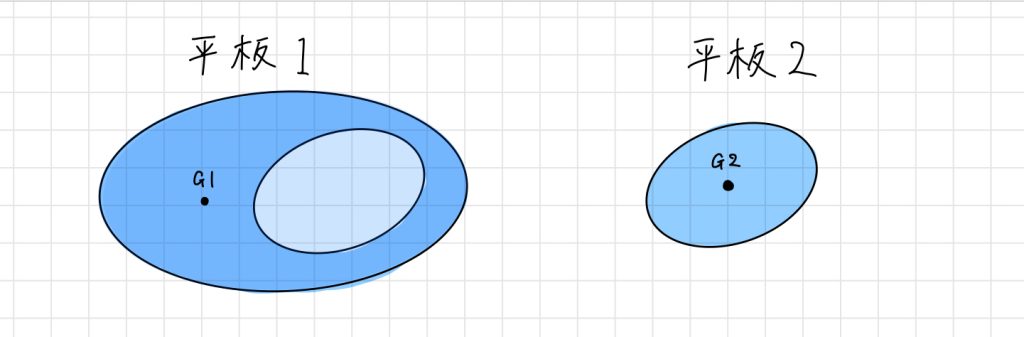
平板1の質量は$\frac{S-S_2}{S}M$、平板2の質量は$\frac{S_2}{S}M$であり、そして重心はそれぞれ$G_1$と$G_2$です。
面積Sの一様な平板の重心は$G$です。これは言い換えると、平板1と平板2を重ね合わせた時、モーメントの中心が$G$になるということになります。視覚的にわかりやすいように、$G_1$、$G_2$に質点のみが存在するとして、下図のようなモーメントが釣り合っているといった状況を考えます。
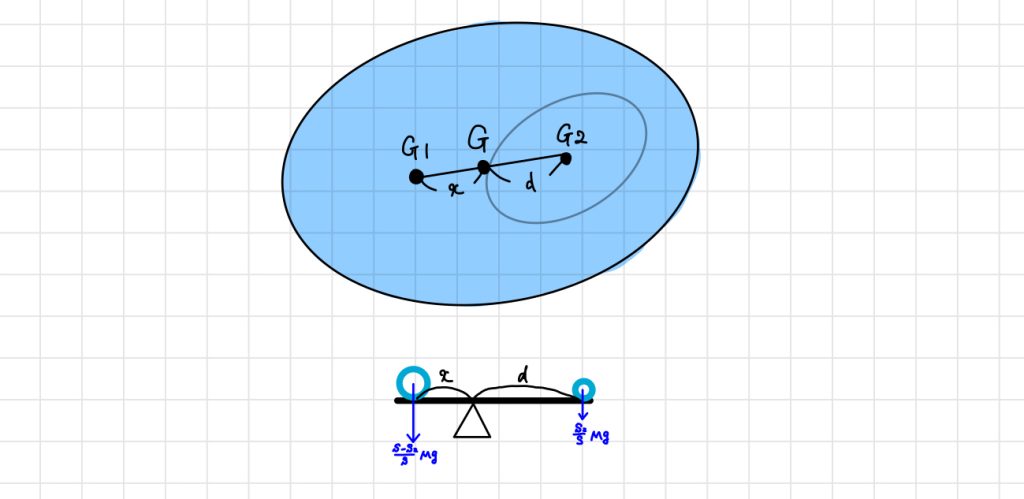
あとはモーメントの釣り合いを式で表すと以下のようになります。
$$\frac{S-S_2}{S}Mg \times x = \frac{S_2}{S}Mg \times d$$
$$x = \frac{S_2}{S-S_2}d$$
となります。
問9

(1)
[解説]
油滴がゆっくりと等速で落下するということは、加速度は0となります。
言い換えると、重力$mg$と抵抗$F$が釣り合うと考えることができます。
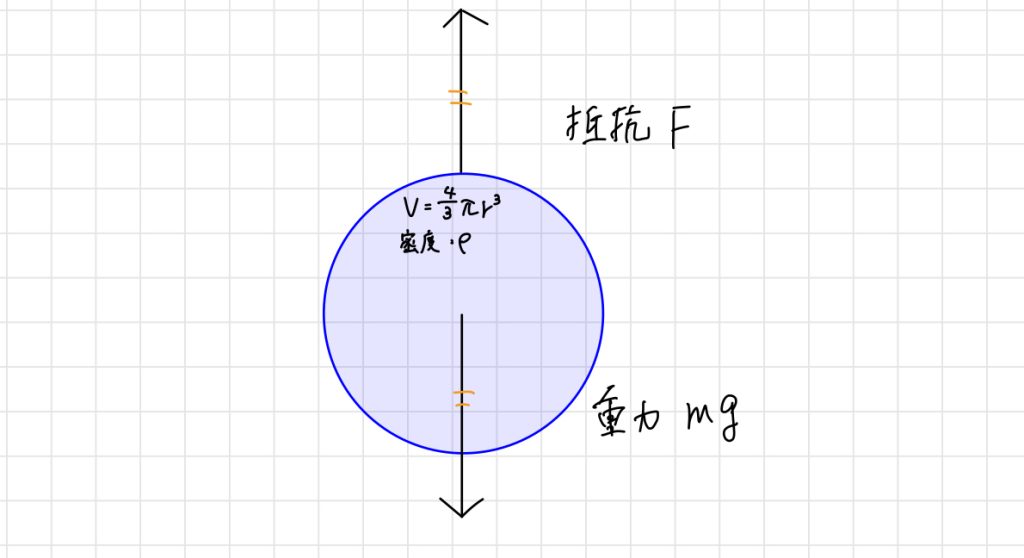
この水滴の半径は$r$より、体積$V$ は$\frac{4}{3} \pi r^3$、密度は$\rho$であるため、質量$m$は、
$$m = V \times \rho$$
$$ = \frac{4}{3} \pi r^3 \times \rho$$
となります。また抵抗$F$は、半径$r$と速さ$v$に比例し、その比例定数は$k$であるため、
$$F = krv$$
と表すことができます。以上より、$F=mg$を以下のように書き換えることができます。
$$krv = \frac{4}{3} \pi r^3 \times \rho$$
$$v = \frac{4 \pi r^2 \rho g}{3k} $$
問10
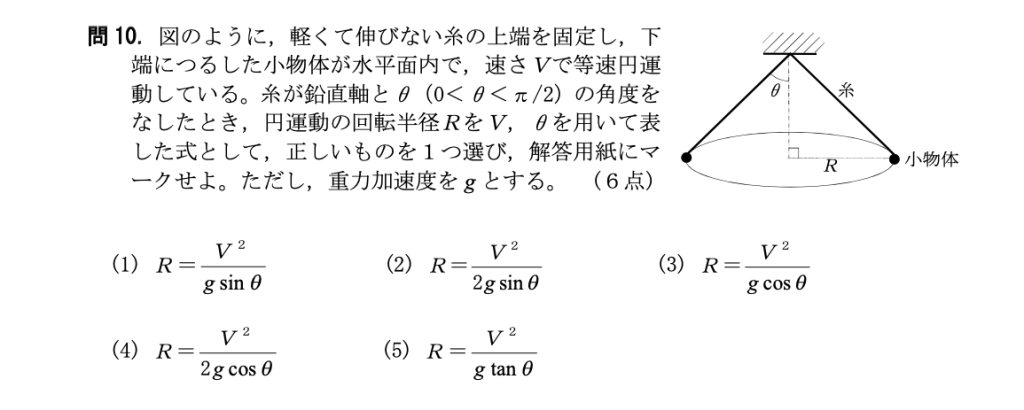
(5)
[解説]
糸に働く張力を$T$、小物体の質量を$m$とすると、水平方向、鉛直方向それぞれの力の釣り合いは以下のようになります。
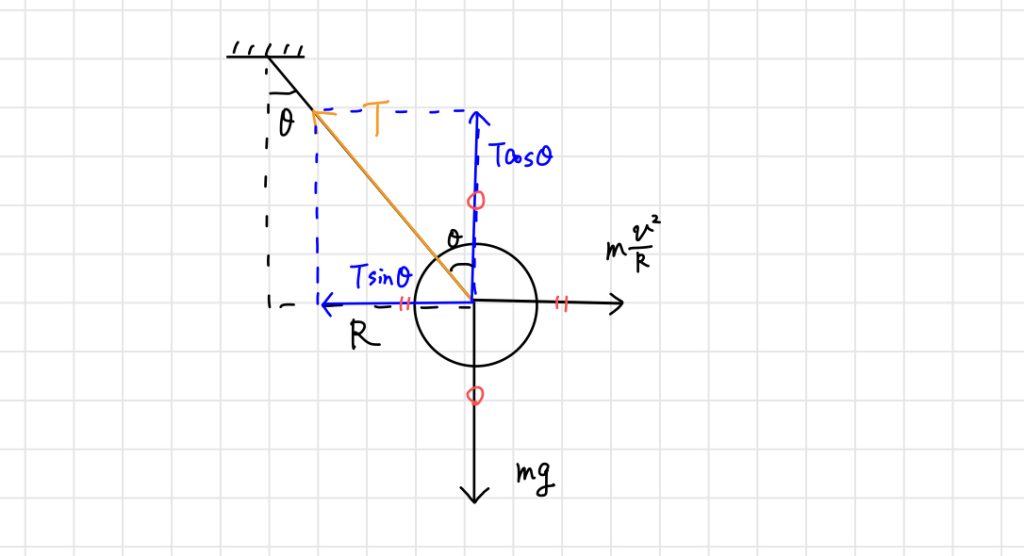
水平方向:$T\sin{\theta} = m\frac{v^2}{R}$ … (1)
鉛直方向:$T\cos{\theta} = mg$ … (2)
(1)式を(2)式で割って$T$を消去すると、
$$\tan{\theta} = \frac{m\frac{v^2}{R}}{mg} = \frac{v^2}{gR}$$
$$R = \frac{v^2}{g\tan{\theta}}$$
となります。
問11
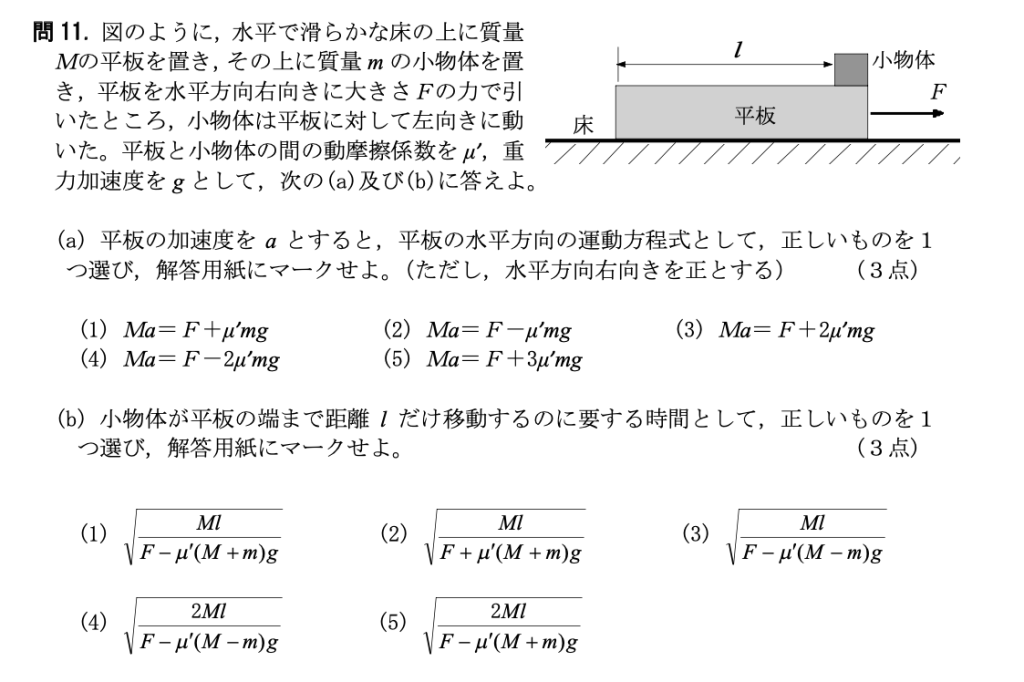
(a) (2) (b) (5)
[解説]
(a)平板及び小物体に働く力は以下のようになっています。
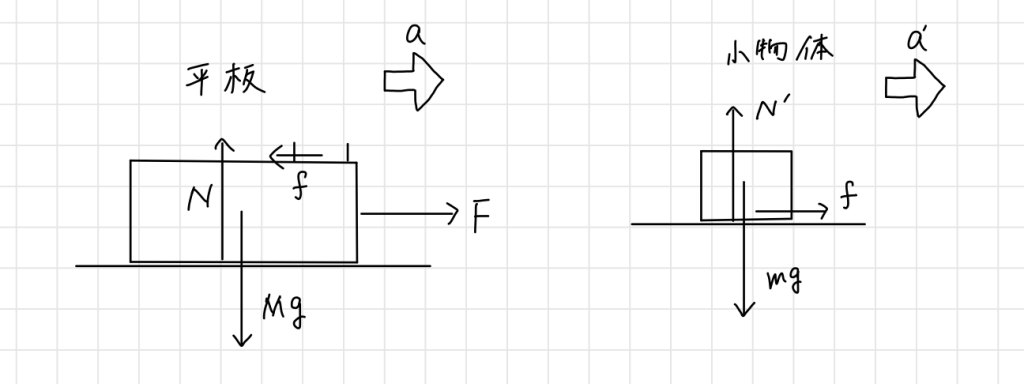
小物体に働く摩擦力を$f$とすると、平板の水平方向の運動方程式は以下のようになります。
$$Ma = F – f$$
ここで、$f = \mu’ N’ = \mu’ mg$
より、
$$Ma = F – \mu’ mg$$
となります。
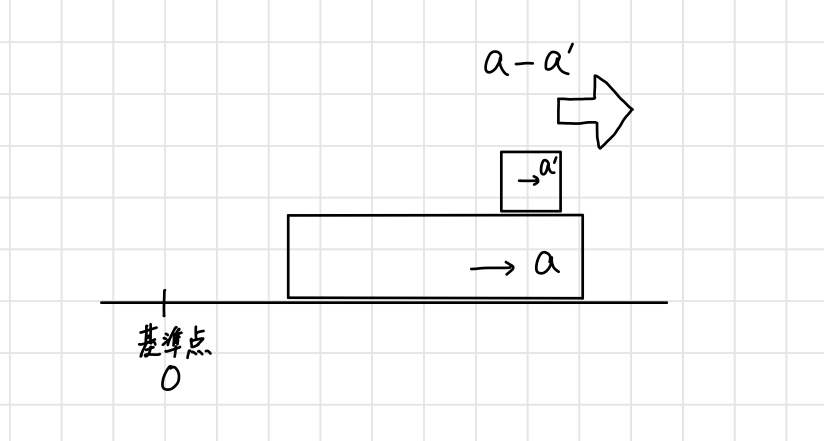
(b)平板の加速度を$a$、小物体の加速度を$a’$とします。これらの運動を平板から離れた位置から観察すると、小物体は床のとある点0に対して、$a-a’$という加速度で移動していると考えることができます。
(a)の解より、
$$Ma = F – \mu’ mg$$
$$a = \frac{F – \mu’ mg}{M}$$
であり、かつ
$$ma’ = \mu’ mg$$より、
$$a – a’ = \frac{F-\mu’ mg}{M} – \mu’ g$$
$$ = \frac{F – \mu’ (M + m)g}{M}$$
となります。ここで距離と速度と時間の公式である$x = v_0 t + \frac{1}{2} a t^2$に代入すると、
$$l = \frac{1}{2} \frac{F – \mu’ (M + m)g}{M} t^2$$
$$t^2 = \frac{2Ml}{F – \mu’ (M + m)g}$$
$$t = \sqrt{\frac{2Ml}{F – \mu’ (M + m)g}}$$となります。
問12

(2)
[解説]
まず時速を秒速に変換します。1時間=3600秒であるため、
$$72 \, [km/h] = \frac{72000 \, [m]}{3600 \, [s]} = 20 \, [m/s]$$
となります。自動車の加速度を$a \, [m/s^2]$、静止するため速度$v$は$0 \, [m/s]$、初速$v_0 = 20 \, [m/s]$、移動距離$x = 40 \, [m]$より、速度と加速度の公式$v^2 – {v_0}^2 = 2ax$に代入すると、
$$v^2 – {v_0}^2 = 2ax$$
$$0^2 – 20^2 = 2 \times a \times 40$$
$$a = -5 \, [m/s^2]$$
となります。この自動車の加速度$a$の絶対値である$5\,[m/s^2]$は重力加速度$10\,[m/s^2]$の$0.5$倍であるとわかります。
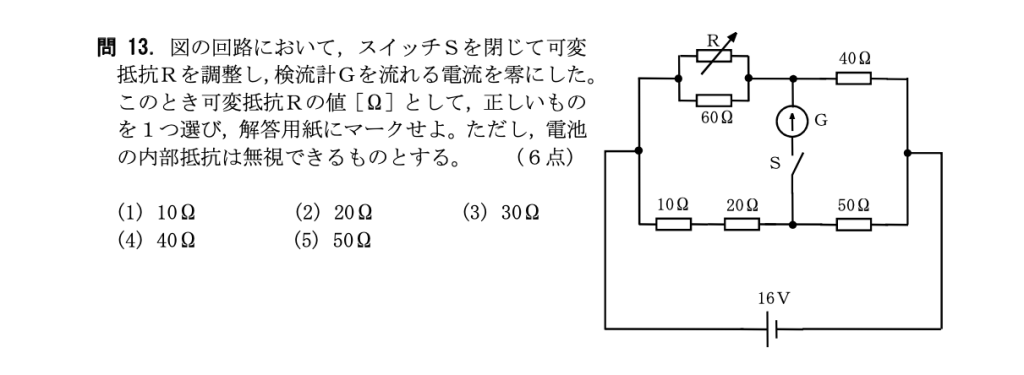
問13
(4)
[解説]
下図のような電気回路において、各抵抗値が
$$\frac{R_1}{R_2} = \frac{R_3}{R_4}$$
といった条件を満たす時、BD間には電流が流れません。
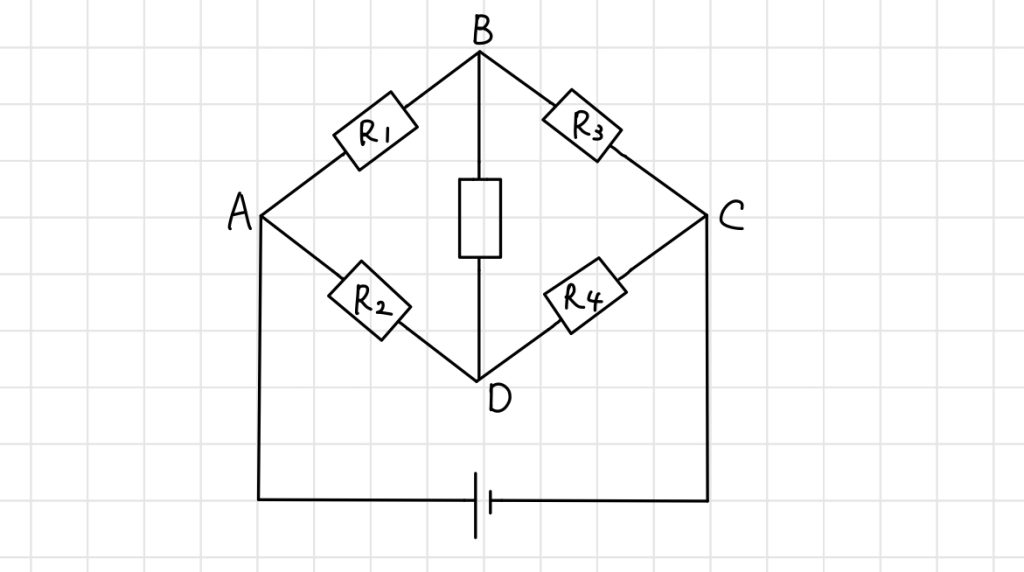

ホイートストンブリッジっていうんやで。
この性質を用いて問題を解きます。
与えられた回路について、抵抗値を下図のように$R_1,R_2,R_3,R_4$とおきます。
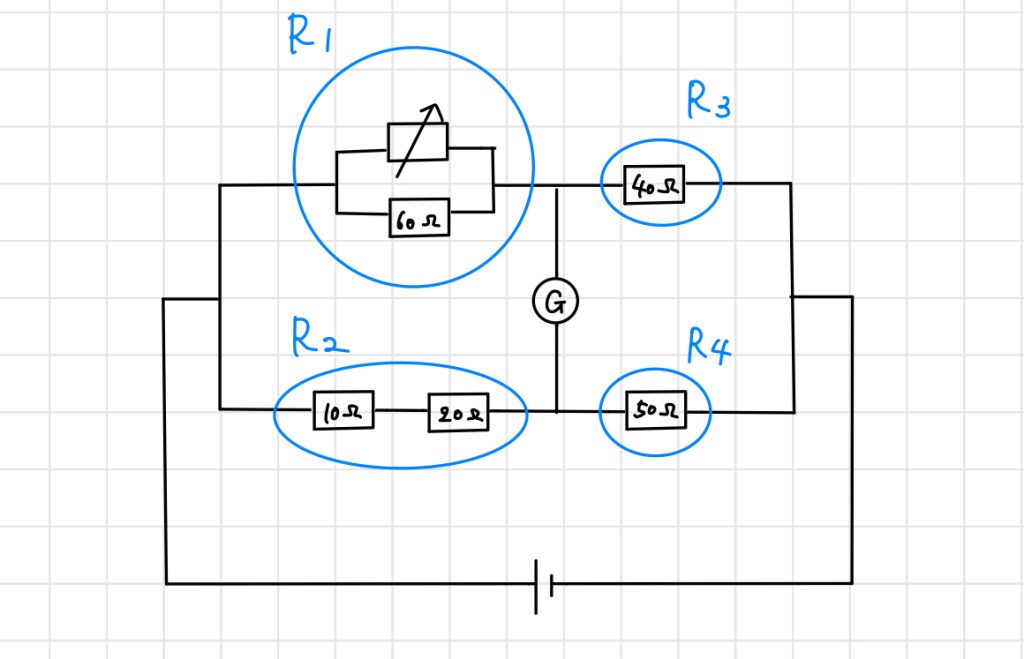
$$R_1 = \frac{60R}{60 + R} \,[\Omega]$$
$$R_2 = 10 + 20 = 30 \,[\Omega]$$
$$R_3 = 40 \,[\Omega]$$
$$R_4 = 50 \,[\Omega]$$
この回路において電流系Gに流れる電流が$0 \,[A]$になるのは、
$$\frac{R_1}{R_2} = \frac{R_3}{R_4}$$
を満たすときです。それぞれに値を代入してやると、
$$\frac{\frac{60R}{60 + R}}{30} = \frac{40}{50}$$
$$R = 40 \,[\Omega]$$
となります。
問14
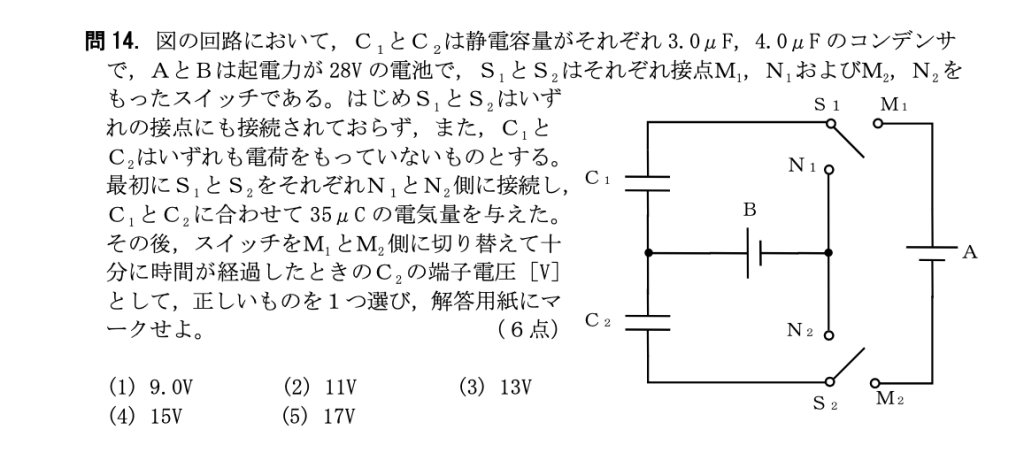
(5)
[解説]
まず$N_1$、$N_2$側に接続した回路について考えます。
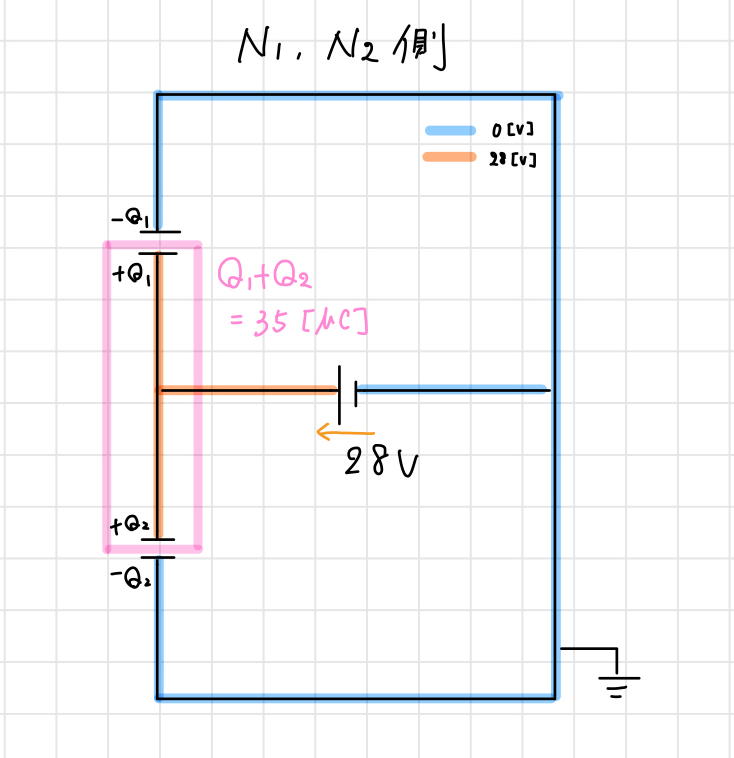
$C_1$、$C_2$に蓄えられる電気量をそれぞれ$Q_1$、$Q_2$とすると、$C_1$と$C_2$合わせて$30\, [\mu C]$の電気量を与えるため、
$$Q_1 + Q_2 = 35 \,[\mu C]$$
となります。次にスイッチを$M_1$、$M_2$側に切り替えます。
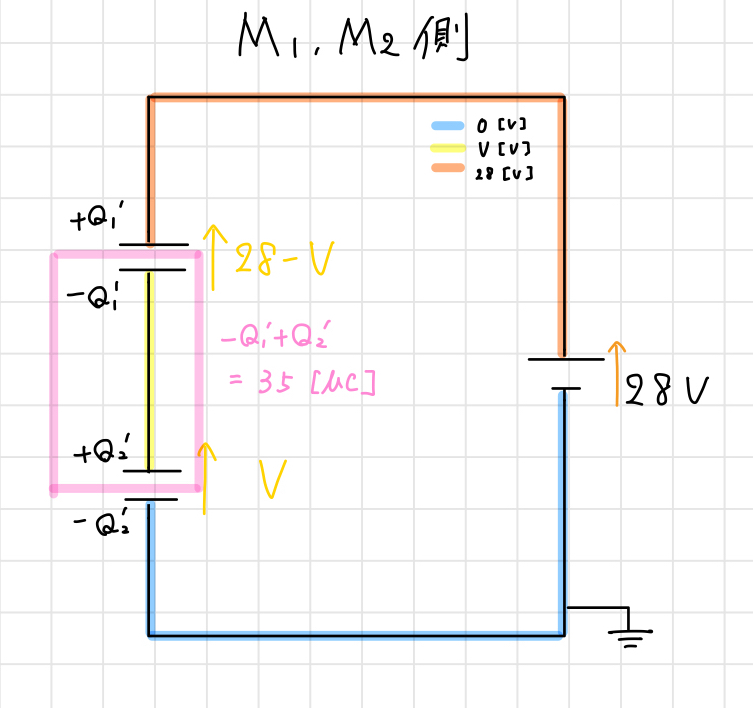
スイッチを切り替えた後に$C_1$、$C_2$に蓄えられる電気量をそれぞれ$Q_{1}’ $、$Q_{2}’$とすると、下図のピンク色の線で囲んだ回路内において電気量が保存されるため、
$$-Q_{1}’ + Q_{2}’ = 35 \,[\mu C] \,\,\, …(1)$$
となります。今回は$N_1$、$N_2$側に接続したときと異なり、十分に時間を経過させるため、$C_2$の端子電圧を$V \,[V]$とすると、$C_1$の端子電圧は$28 – V \,[V]$となります。よって、
$$Q_{1}’ = 3.0 \mu \times (28 – V) \,[\mu C]$$
$$Q_{2}’ = 4.0 \mu \times 28 \,[\mu C]$$
となり、これらを(1)式に代入すると、
$$-3.0\mu \times (28 – V) + 4.0 \mu \times 28 = 35 \,[\mu C]$$
$$V = 17 \,[V]$$
となります。
問15
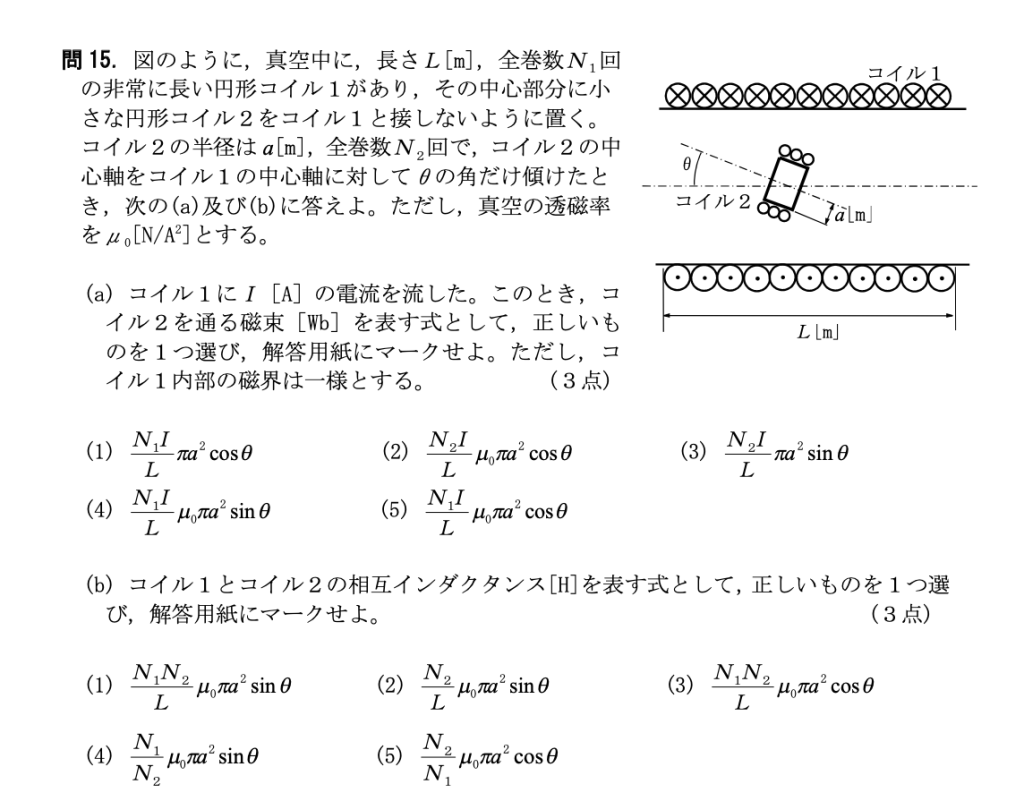
(a) (5) (b)(3)
[解説]
(a)長さ$L$、全巻数$N_1$のソレノイドに電流$I$を流した時の磁束密度$B$は、真空の透磁率$\mu_0$を用いて、
$$B = \frac{\mu_0 N_1 I}{L}$$
と表すことができます。ここで、コイルは半径$a$で、中心軸が$\theta$だけ傾いているため、有効面積$S$は、
$$S = \pi a^2 \cos{\theta}$$
となります。よって、コイル2を通る磁束$\Phi_2$は、
$$\Phi_2 = BS$$
$$ = \frac{\mu_0 N_1 I}{L} \times \pi a^2 \cos{\theta}$$
$$ = \frac{N_1 I}{L} \mu_0 \pi a^2 \cos{\theta}$$
となります。
(b)コイル1とコイル2の相互インダクタンスを$M$とおくと、コイル2に生じる起電力$V_2$は、
$$V_2 = -M \frac{\Delta I}{\Delta t} \,\,\, …(1)$$
と表すことができます。ここで、起電力$V_2$を(a)で求めた$\Phi_2$を用いて表すと、
$$V_2 = – N_2\frac{\Delta \Phi_2}{\Delta t}$$
$$ = -N_2\frac{\Delta(\frac{N_1 I}{L} \mu_0 \pi a^2 \cos{\theta})}{\Delta t}$$
$$ = -\frac{N_1 N_2}{L} \mu_0 \pi a^2 \cos{\theta} \frac{\Delta I}{\Delta t} \,\,\, …(2)$$
となります。(1)式と(2)式を比較することにより、
$$M = \frac{N_1 N_2}{L} \mu_0 \pi a^2 \cos{\theta}$$
となります。



コメント